Skip to main content

Reading Notes: Copulas as High-Dimensional Generative Models: Vine Copula Autoencoders

Copulas as High-Dimensional Generative Models: Vine Copula Autoencoders

This post is a work through for this paper by Natasa et al: Copulas as High-Dimensional Generative Models: Vine Copula Autoencoders, one can find the paper here.

Introduction

The authors introduced vine copula autoencoder (VCAE) as a flexible generative model for high-dimensional distributions. The model is simply built in a three-step procedure:

  1. Train an autoencoder to compress the data into a lower dimensional representations;
  2. Estimate the encoded representation's distribution with vine copulas;
  3. Combine the distribution and the decoder to generate new data points.

The authors claimed that this generative model has 3 advantages compared to Generative Adversarial Nets (GANs) and Variational Autoencoders (VAEs):

  1. It offers modeling flexibility by avoiding most distributional assumptions in contrast to VAEs;
  2. Training and sampling procedures for high-dimensional data are straightforward;
  3. It can be used as a plug-in allowing to turn any AE into generative model, simultaneously allowing it to serve other purposes (e.g., denoising, clustering).

Vine copula autoencoders

The basic procedure of training vine copula autoencoders (VCAE) is described in Fig 1. The first building block of VCAE is a regular autoencoder, with a compressed latent representation . One major difference between VCAE and VAE is that VAEs assume a simple prior (like Gaussian) to , however, VCAEs doesn't make such assumptions, they deal with the distribution entirely with vine copula training.

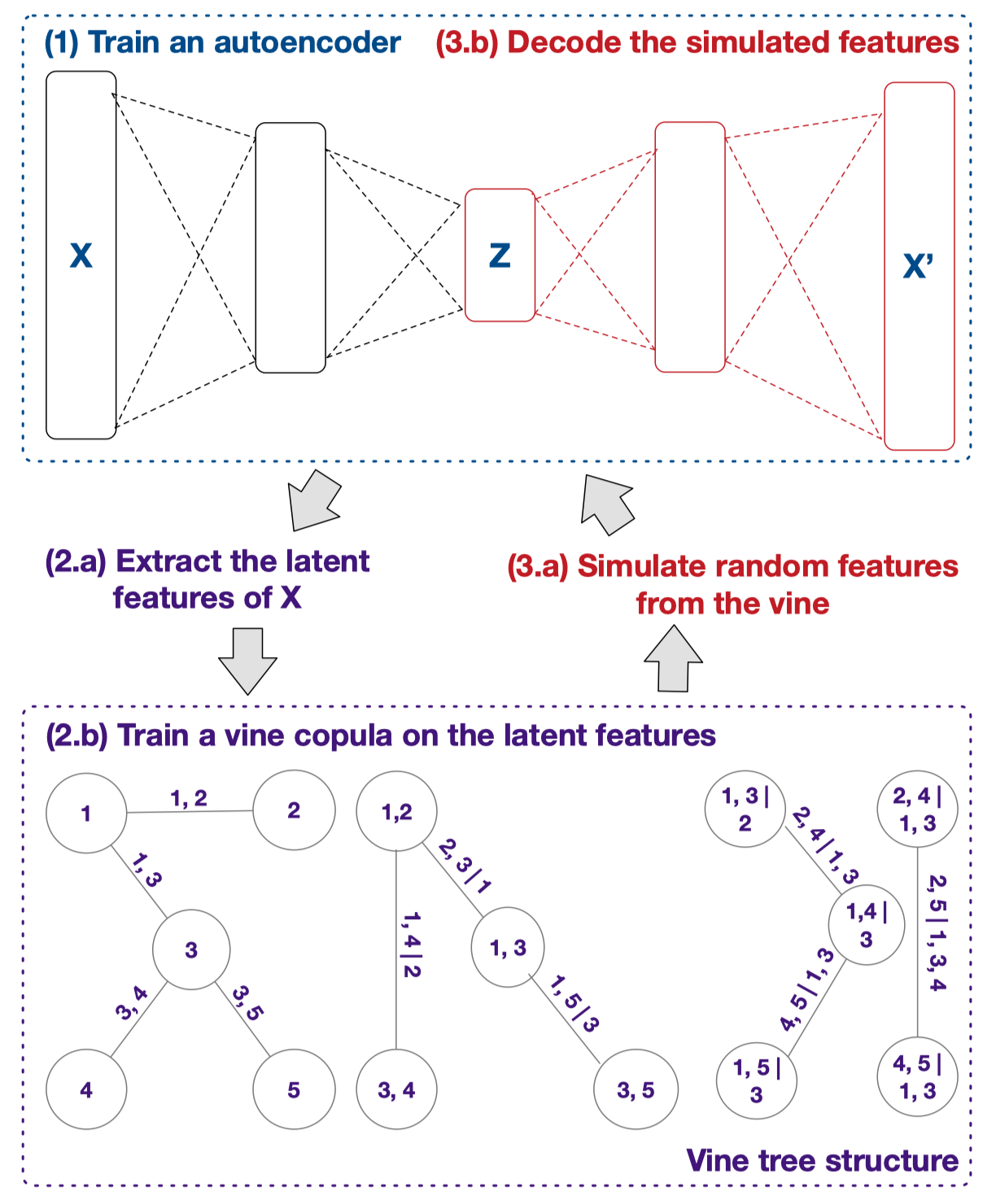
vine_copula_illu

Fig 1: Conceptual illustration of a VCAE.

If we use to represent the autoencoder, then the job of vine copula is to learn the distribution of such that it can generate samples using .

Vine copulas

The major contribution lies in the application of vine copulas.

Copulas and its basic property

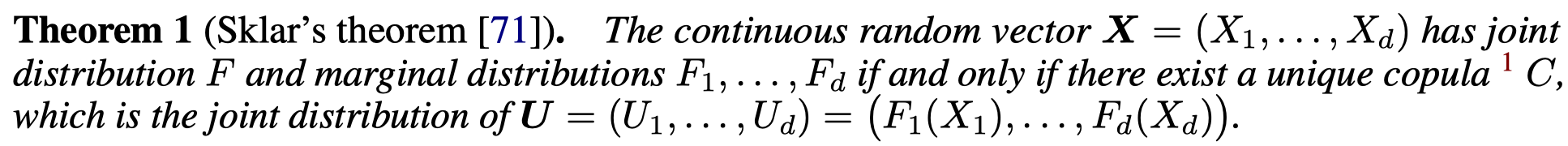
vine_copula_thm

The Sklar's theorem tells us that copulas allow us to decompose a joint density into a product between the marginal densities and the dependence structure represented by the copula density . i.e., assuming that all densities exist, we can write , where and are the densities corresponding to respectively.

This implies that the generating procedure can be done in two steps:

  1. Estimating the marginal distributions;
  2. Using the estimated distributions to construct pseudo-observations via the probability integral transform before estimating the copula density.

Vine copulas construction

The pair-copula constructions (PCCs), also called vine copulas, is used in this paper as pair wise copula construction is much more feasible compared to joint modeling all variables.

PCCs model the joint distribution of a random vector by decomposing the problem into modeling pairs of conditional random variables, making the construction of complex dependencies both flexible and yet tractable.

Lets consider an example with 3 random variables , the joint density of can be decomposed as

Where s represents the marginal distributions of , and represents the pair copula between and , which also represents the dependencies. Note that represents conditional copula/dependency.

For the details of how vine copulas are estimated, or why they would work, one can read the workshop slides by Nicole et al. in NIPS workshop 2011.

The training and generating procedure of vine copula

Fig 2 illustrate the estimation and sampling procedure for a (conditional) pair copula.

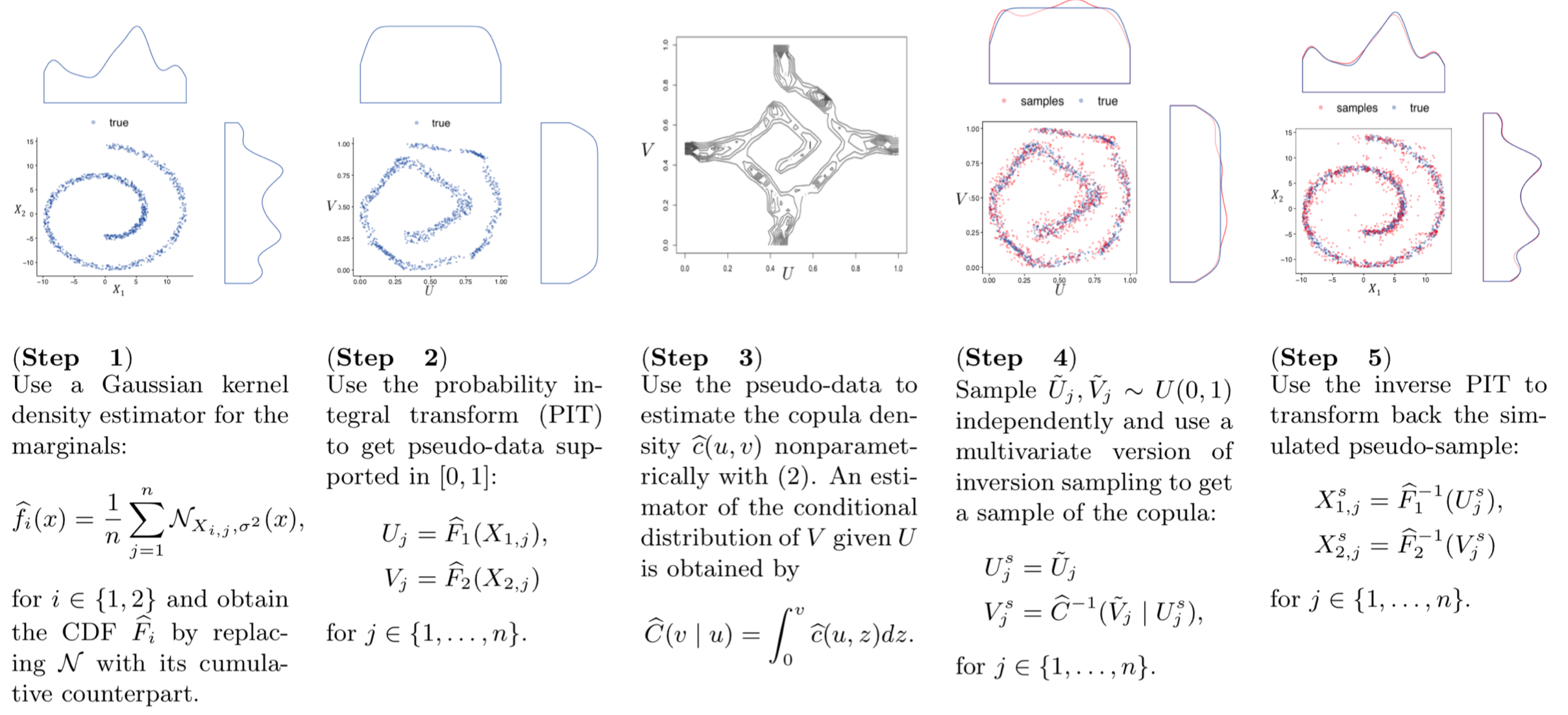
vine_copula_estmation

Fig 2: Estimation and sampling algorithm for a pair copula

Note that plenty of the algorithms for vine copula estimation and generation are implemented in C++ package vinecopulib.

 

Conclusion

The authors proposed a new way for deep generative modeling using vine copulas with a very clever combination of traditional vine copula estimation and a regular auto encoder modeling. This inspires us to apply more old-school techniques on the latent low-dimensional features learned by deep networks like autoencoders.

Comments

Post a Comment

Popular posts from this blog

Reading notes: On the Connection Between Adversarial Robustness and Saliency Map Interpretability

Etmann et al. Connection between robustness and interpretability On the Connection Between Adversarial Robustness and Saliency Map Interpretability Advantage and Disadvantages of adversarial training? While this method – like all known approaches of defense – decreases the accuracy of the classifier, it is also successful in increasing the robustness to adversarial attacks Connections between the interpretability of saliency maps and robustness? saliency maps of robustified classifiers tend to be far more interpretable, in that structures in the input image also emerge in the corresponding saliency map How to obtain saliency maps for a non-robustified networks? In order to obtain a semantically meaningful visualization of the network’s classification decision in non-robustified networks, the saliency map has to be aggregated over many different points in the vicinity of the input image. This can be achieved either via averaging saliency maps of noisy versions of the image (Smilkov...
Post a Comment
Read more

Reading Notes: Probabilistic Model-Agnostic Meta-Learning

Probabilistic Model-Agnostic Meta-Learning Reading Notes: Probabilistic Model-Agnostic Meta-Learning This post is a reading note for the paper "Probabilistic Model-Agnostic Meta-Learning" by Finn et al. It is a successive work to the famous MAML paper , and can be viewed as the Bayesian version of the MAML model. Introduction When dealing with different tasks of the same family, for example, the image classification family, the neural language processing family, etc.. It is usually preferred to be able to acquire solutions to complex tasks from only a few samples given the past knowledge of other tasks as a prior (few shot learning). The idea of learning-to-learn, i.e., meta-learning, is such a framework. What is meta-learning? The model-agnostic meta-learning (MAML) [1] is a few shot meta-learning algorithm that uses gradient descent to adapt the model at meta-test time to a new few-shot task, and trains the model parameters at meta-training time to enable rapid adap...
Post a Comment
Read more

Evaluation methods for recommender systems

There are plenty of recommender systems available, the question is, for a specific recommendation problem, which recommender system model to use? The prediction accuracy (ratio of correct predicted items) is a straightforward approach, however, this is in most cases doesn't give a good indication on how 'good' the model is? Because usually, the ratings are somehow ordinal, which means the ratings are ordered instead of categorical, a prediction of 4 star is better than prediction of 5 star for a ground truth of 3 star, while when evaluate with accuracy, 4-star prediction and 5-star are treated equal -- incorrect prediction. There are plenty of better evaluation methods available,  in this post, I will introduce some of them. But first of all, lets review some basic concepts in model evaluation. To simplify our settings, lets say that we have a binary classification model, it made predictions on a test dataset, the prediction result is shown in Figure 1. Then the pr...
1 comment
Read more